Techniques for Computing Exact Hausdorff Measure with Application to a Sierpinski Sponge in $\mathbb{R}^3$
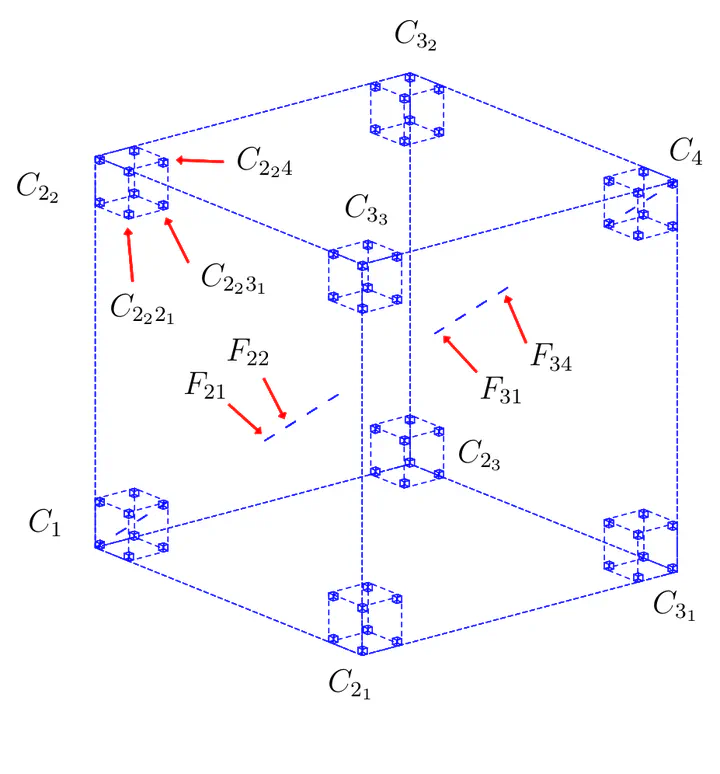 This figure shows unit cube C∅ superimposed on the first and second levels of the construction of the Sierpinski sponge whose Hausdorff measure we are computing. The projection of the second level of the construction onto one of the main diagonals of the sponge is also shown.
This figure shows unit cube C∅ superimposed on the first and second levels of the construction of the Sierpinski sponge whose Hausdorff measure we are computing. The projection of the second level of the construction onto one of the main diagonals of the sponge is also shown.Abstract
In this dissertation we aim to perform a detailed study of techniques for
the analysis of the exact $s$-dimensional Hausdorff measure of fractal sets and try
to provide a reasonably comprehensive review of the required background. An emphasis
is placed on results pertaining to local density of sets and we show how these provide
a link to the more global concept of Hausdorff measure. A new result is provided
which states that if $K$ is a self-similar set satisfying the open set condition,
then $\mathcal{H}^s(K \cap U) \leq |U|^s$ for all Borel $U$, also implying that
$\overline{D}_c(K, x) \leq 1$ for all $x$, where $\mathcal{H}(E)$
and $\overline{D}_c(E, x)$ refer to the $s$-dimensional Hausdorff measure of some
set $E$ and the local convex density of $E$ at a point $x$ respectively. Based on the
work of Zuoling Zhou and Min Wu, we provide new calculations for the exact Hausdorff
measure of both a Sierpinski carpet in $\mathbb{R}^2$ and a Sierpinski sponge
in $\mathbb{R}^3$. In the final chapter we take a look at how the Hausdorff
measure behaves when measuring the invariant sets associated with special types
of iterated function systems known as iterated function systems with condensation
and also provide a brief discussion on the calculation of the packing measure of
a self-similar set.
Type